RLC 회로는 직렬일 때는 KVL을 적용하고, 병렬일 때는 KCL을 적용합니다. 직렬일 때 구한 i(t)는 유도기에 흐르는 전류이고 병렬일 때 구한 v(t)는 축전기에 걸리는 전압입니다. 식을 통해 유도기에 걸리는 전압, 축전기에 흐르는 전류등을 구하면 됩니다.

목차
1. 직렬 RLC 회로 i(t) 구하기
2. 직렬 RLC 회로 문제풀이법
3. 예제 풀이
1. 직렬 RLC 회로 i(t) 구하기
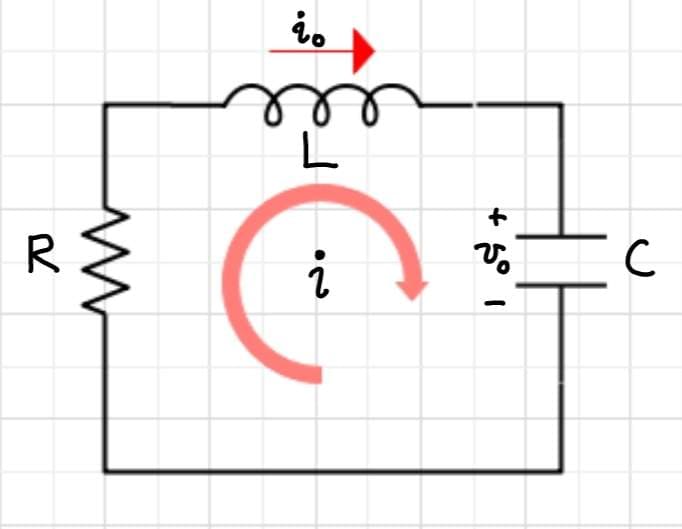
위 회로에 KVL 적용하면
$$iR+L {di\over dt}+{1\over C}\int^{t}_{-\infty} i(\tau) d\tau=0\dots1번$$
위 식을 통해 우리는 i의 변화율의 초기값을 알 수 있습니다.
$${di(0)\over dt}=-{1\over L}(RI_0+V_0)$$
1 번식을 i에 대해 미분하면
$$R {di\over dt}+L {d^2i\over dt^2}+{1\over C} i=0$$
정리하면 Homogeneous Linear ODE가 됩니다. 공업수학 내용이므로 자세하게 설명하지는 않겠습니다.
$${d^2i\over dt^2}+{R\over L}{di\over dt}+{1\over LC} i=0\dots2번$$
또한 상수로만 이루어진 Homogeneous Linear ODE이므로 해의 기본꼴은 아래와 같이 됩니다.
미분을 몇 번 해보면 이해가능합니다.
$$i=Ae^{st}$$
그래서 2 번식에 $i=Ae^{st}$을 대입하고 정리하면
$$Ae^{st}(s^2+{R\over L} s+{1\over LC})=0$$
$Ae^{st}$은 0이 아니므로
$$s^2+{R\over L} s+{1\over LC}=0$$
$\alpha={R\over 2L}, w_0={1\over \sqrt {LC}}$으로 변환하면 아래와 같이 쓸 수 있습니다.
$$s^2+2\alpha s+w_0^2=0$$
해:$s_1=-\alpha+\sqrt {\alpha^2-w_0^2}, s_2=-\alpha-\sqrt {\alpha^2-w_0^2}$
$s_1, s_2$는 자연빈도(natural frequencies)라고 하고 회로의 자연응답과 연관성을 가집니다.
위의 식은 보조방정식(auxiliary equation)으로 근에 따라 미분방정식의 일반해가 달라집니다.
1. 서로 다른 두실근 ($\alpha> w_0 $) 일 때 overdamped case(과도감쇄)
2. 중근 ($\alpha=w_0 $) 일 때 critically damped case(임계감쇄)
3. 켤레 복소근 ($\alpha <w_0 $) 일 때 underdamped case(저감 쇄)

overdamped case ($\alpha> w_0 $)
일반해는
$$i(t)=A_1e^{s_1t}+A_2e^{s_2t}$$
critically damped case ($\alpha=w_0 $)
일반해
$$i(t)=(A_2+tA_1) e^{-\alpha t}$$
underdamped case ($\alpha <w_0 $)
$s_1=-\alpha+\sqrt {\alpha^2-w_0^2}=-\alpha+jw_d$
$s_2=-\alpha-\sqrt {\alpha^2-w_0^2}=-\alpha-jw_d$
일반해
$$i(t)=e^{-\alpha t}(B_1 cosw_dt+B_2 sinw_dt)$$
2. 직렬 RLC 회로 문제풀이법
1.$v(0^+), i(0^+)$과 $di(0)/dt$ 구하기 (미정계수 구할 때 쓰임)
2. KVL로 미분방정식 만들기
3. 특성방정식의 근을 통해 미분방정식의 일반해 구하기
4. 1번에서 구한 값으로 i(t)의 미정계수 해결하기
3. 예제 풀이
Practice Problem 8.4

1.$v(0^+), i(0^+)$과 di(0)/dt 구하기
$$i(0^-)=i(0^+)=10A$$
$$v(0^+)=v(0^-)=0V$$
$${di(0)\over dt}=-{1\over L}(Ri+v)=-1(5\Omega\times10A+0V)=-50A/s$$
2. KVL로 미분방정식 만들기
$$Ri+L {di\over dt}{1\over C}+\int^{t}_{-\infty} i(\tau) d\tau=0$$
$${d^2i\over dt^2}+{R\over L}{di\over dt}+{1\over LC} i=0$$
$${d^2i\over dt^2}+{5\Omega\over 1H}{di\over dt}+{1\over 1H\times1/9F} i=0$$
$i=Ae^{st}$을 대입하면
$$Ae^{st}(s^2+5s+9)=0$$
$$s^2+5s+9=d$$
${\sqrt {11}\over 2}=1.6583$이므로
$$s_1=-2.5+1.6583j, s_2=-2.5+1.6583j$$
3. 특성방정식의 근을 통해 미분방정식의 일반해 구하기
$$i(t)=e^{-\alpha t}(B_1 cosw_dt+B_2 sinw_dt)$$
$$=e^{-2.5t}(B_1 cos(1.6583t)+B_2 sin(1.6583t))A$$
4. 1번에서 구한 값으로 i(t)의 미정계수 해결하기
'공학 > 전기회로' 카테고리의 다른 글
| [회로이론] 병렬 RLC 회로 유도와 예제풀이 (2) | 2023.10.26 |
|---|---|
| [회로이론] RLC 회로에서 초기값과 나중값 심화 예제 풀기 (1) | 2023.10.13 |
| [회로이론] 계단 응답 RL 회로 심화 예제 풀이 (0) | 2023.09.27 |
| [회로이론] 계단 응답 RC 회로 심화 예제풀이 (1) | 2023.09.26 |
| [회로 이론] RC 회로, RL 회로 심화 예제 풀이 (0) | 2023.09.24 |



